Publications:
see the google scholar link for the latest
Using Activity to Compartmentalize Binary Mixtures
By Lauersdorf, N. J., Nazockdast, E., & Klotsa, D. (2024).
Doi: https://doi.org/10.48550/arXiv.2407.07826
We computationally study suspensions of slow and fast active Brownian particles that have undergone motility induced phase separation and are at steady state. Such mixtures, of varying non-zero activity, remain largely unexplored even though they are relevant for a plethora of systems and applications ranging from cellular biophysics to drone swarms. Our mixtures are modulated by their activity ratios (PeR), which we find to encode information by giving rise to three regimes, each of which display their unique emergent behaviors. Specifically, we found non-monotonic behavior of macroscopic properties, e.g. density and pressure, as a function of activity ratio, microphase separation of fast and slow particle domains, increased fluctuations on the interface and severe avalanche events compared to monodisperse active systems. Our approach of simultaneously varying the two activities of the particle species allowed us to discover these behaviors and explain the microscopic physical mechanisms that drive them.
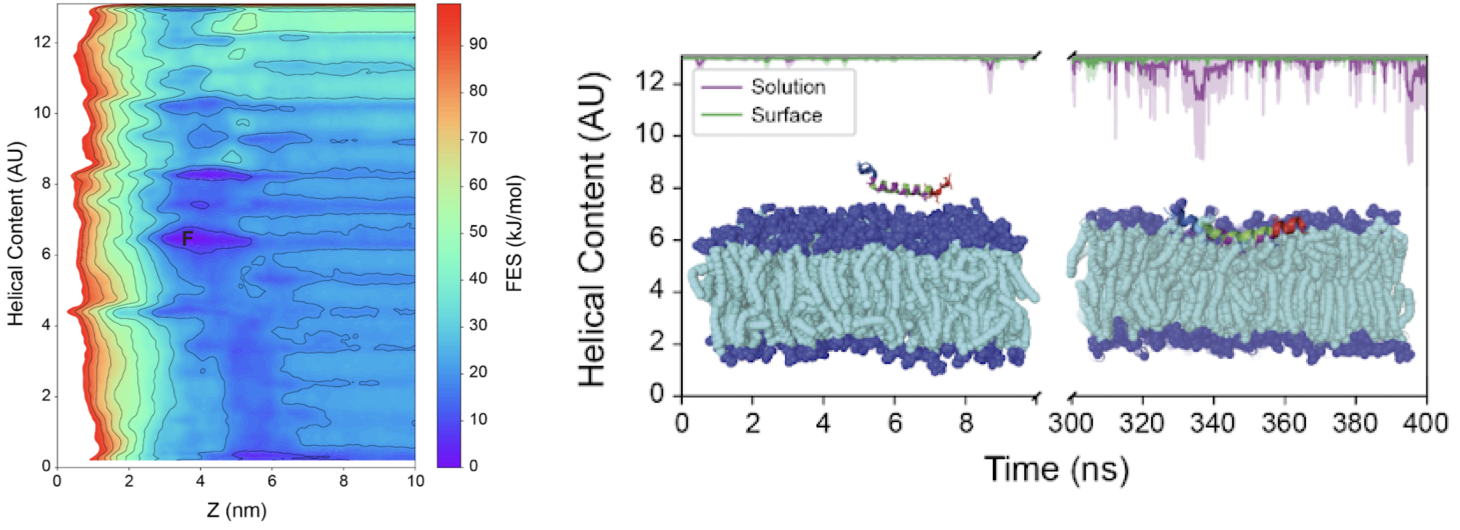
Charge distribution and helical content tune the binding of septin’s amphipathic helix domain to lipid membranes.
By Edelmaier, C. J., Klawa, S. J., Mofidi, S. M., Wang, Q., Bhonge, S., Vogt, E. J., ... & Nazockdast, E. (2024).
Submitted to Biophys. J. Doi: https://doi.org/10.1101/2024.07.05.602292
Septins are a class of cytoskeletal proteins that preferentially bind to domains of micron-scale curvature on the cell membrane. Studies have shown that amphipathic helix (AH) domains in septin oligomers are essential for septin curvature sensing. Yet, the underlying mechanochemical interactions that modulate this curvature sensing remain ambiguous. Here we use all-atom molecular dynamics alongside a metadynamics enhanced sampling approach to bridge the gap between time and length scales required to optimize and validate experimental design of amphipathic helices. Simulations revealed that the local charge on the termini of an 18-amino-acid AH peptide impacts its helical content and positioning within lipid membranes. These computational observations are confirmed with experiments measuring the binding of synthetic AH constructs with variable helical content and charged termini to lipid vesicles. Taken together, these results identify the helical content of amphipathic helices as a regulator of septin binding affinity to lipid membranes. Additionally, we examined an extended AH sequence including 8 amino acids upstream and downstream of the minimal 18-amino-acid-long AH domain to more closely mimic the native protein in simulations and experiments. Simulations and experiments show that the extended peptide sequence adopts a strong alpha-helical conformation when free in solution, giving rise to a higher affinity to lipid membranes than that of the shorter AH sequence. Together, these results provide insight into how the native septin proteins interact with membranes, and establish general design principles that can guide the interaction of future synthetic materials with lipid membranes in a programmable manner.
A reciprocal theorem for biphasic poro-viscoelastic materials
By M. Moradi, W. Shi and E. Nazockdast
Accepted for publication in J. Fluid Mechanics
In studying the transport of inclusions in multi-phase systems we are often interested in integrated quantities such as the net force and the net velocity of the inclusions. In the reciprocal theorem, the known solution to the first and typically easier boundary value problem is used to compute the integrated quantities, such as the net force, in the secondproblem without the need to solve that problem. Here, we derive a reciprocal theoremfor poro-viscoelastic (or biphasic) materials which are composed of a linear compressiblesolid phase, permeated by a viscous fluid. As an example, we analytically calculate the time-dependent net force on a rigid sphere in response to point-forces applied to the elastic network and the Newtonian fluid phases of the biphasic material. We show that when the point-force is applied to the fluid phase, the net force on the sphere evolves over timescales that are independent of the distance between the point-force and the sphere; in comparison, when the point-force is applied to the elastic phase the timescale for force development increases quadratically with the distance, in line with the scaling of poroelastic relaxation time. Finally, we formulate and discuss how the reciprocal theorem can be applied to other areas, including (i) calculating the network slip on the sphere’s surface, (ii) computing the leading order effects of nonlinearities in the fluid and network forces and stresses, and (iii) calculating self-propulsion in biphasic systems.
The drag of a filament moving in a supported spherical bilayer
By W. Shi, M. Moradi and E. Nazockdast
Journal of Fluid Mechanics, 979, A6. DOI: https://doi.org/10.1017/jfm.2023.1036
Many of the cell membrane's vital functions are achieved by the self-organization of the proteins and biopolymers embedded in it. The protein dynamics is in part determined by its drag. A large number of these proteins can polymerize to form filaments. In vitro studies of protein–membrane interactions often involve using rigid beads coated with lipid bilayers, as a model for the cell membrane. Motivated by this, we use slender-body theory to compute the translational and rotational resistance of a single filamentous protein embedded in the outer layer of a supported bilayer membrane and surrounded on the exterior by a Newtonian fluid. We first consider the regime where the two layers are strongly coupled through their inter-leaflet friction. We find that the drag along the parallel direction grows linearly with the filament's length and quadratically with the length for the perpendicular and rotational drag coefficients. These findings are explained using scaling arguments and by analysing the velocity fields around the moving filament. We then present and discuss the qualitative differences between the drag of a filament moving in a freely suspended bilayer and a supported membrane as a function of the membrane's inter-leaflet friction. Finally, we briefly discuss how these findings can be used in experiments to determine membrane rheology. In summary, we present a formulation that allows computation of the effects of membrane properties (its curvature, viscosity and inter-leaflet friction), and the exterior and interior three-dimensional fluids’ depth and viscosity on the drag of a rod-like/filamentous protein, all in a unified theoretical framework.
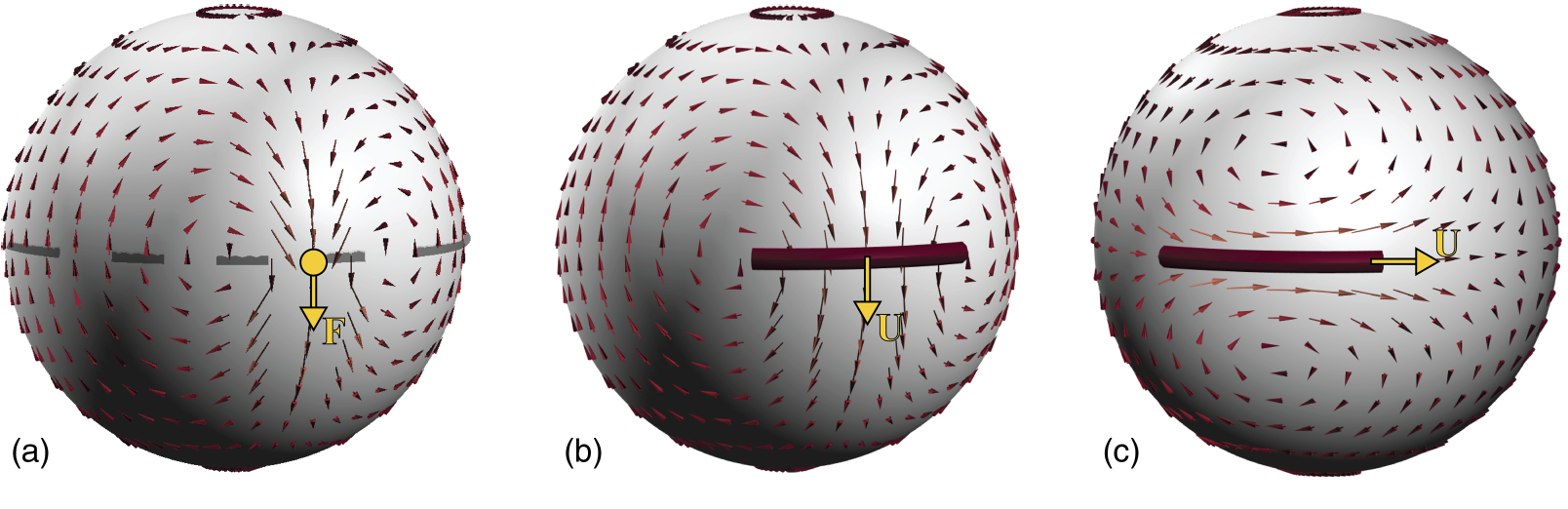
Laser ablation and fluid flows reveal the mechanism behind spindle and centrosome positioning
by H-Y Wu, G. Kabacaoğlu , E. Nazockdast, Huan-Cheng Chang , M. J. Shelley, D. J. Needleman
Nature Physics (2023), https://doi.org/10.1038/s41567-023-02223-z
Few techniques are available for studying the nature of forces that drive subcellular dynamics. Here we develop two complementary ones. The first is femtosecond stereotactic laser ablation, which rapidly creates complex cuts of subcellular structures and enables precise dissection of when, where and in what direction forces are generated. The second is an assessment of subcellular fluid flows by comparison of direct flow measurements using microinjected fluorescent nanodiamonds with large-scale fluid-structure simulations of different force transduction models. We apply these techniques to study spindle and centrosome positioning in early Caenorhabditis elegans embryos and to probe the contributions of microtubule pushing, cytoplasmic pulling and cortical pulling upon centrosomal microtubules. Based on our results, we construct a biophysical model to explain the dynamics of centrosomes. We demonstrate that cortical pulling forces provide a general explanation for many behaviours mediated by centrosomes, including pronuclear migration and centration, rotation, metaphase spindle positioning, asymmetric spindle elongation and spindle oscillations. This work establishes methodologies for disentangling the forces responsible for cell biological phenomena.
Curvature sensing as an emergent property of multiscale assembly of septins
by W. Shi, K. S. Cannon, B. N. Curtis, C. Edelmaier, A. S. Gladfelter, E. Nazockdast
In PNAS, Vol. 120, No. 6, https://doi.org/10.1073/pnas.2208253120
The ability of cells to sense and communicate their shape is central to many of their functions. Much is known about how cells generate complex shapes, yet how they sense and respond to geometric cues remains poorly understood. Septins are GTP-binding proteins that localize to sites of micrometer-scale membrane curvature. Assembly of septins is a multistep and multiscale process, but it is unknown how these discrete steps lead to curvature sensing. Here, we experimentally examine the time-dependent binding of septins at different curvatures and septin bulk concentrations. These experiments unexpectedly indicated that septins’ curvature preference is not absolute but rather is sensitive to the combinations of membrane curvatures present in a reaction, suggesting that there is competition between different curvatures for septin binding. To understand the physical underpinning of this result, we developed a kinetic model that connects septins’ self-assembly and curvature-sensing properties. Our experimental and modeling results are consistent with curvature-sensitive assembly being driven by cooperative associations of septin oligomers in solution with the bound septins. When combined, the work indicates that septin curvature sensing is an emergent property of the multistep, multiscale assembly of membrane-bound septins. As a result, curvature preference is not absolute and can be modulated by changing the physicochemical and geometric parameters involved in septin assembly, including bulk concentration, and the available membrane curvatures. While much geometry-sensitive assembly in biology is thought to be guided by intrinsic material properties of molecules, this is an important example of how curvature sensing can arise from multiscale assembly of polymers.
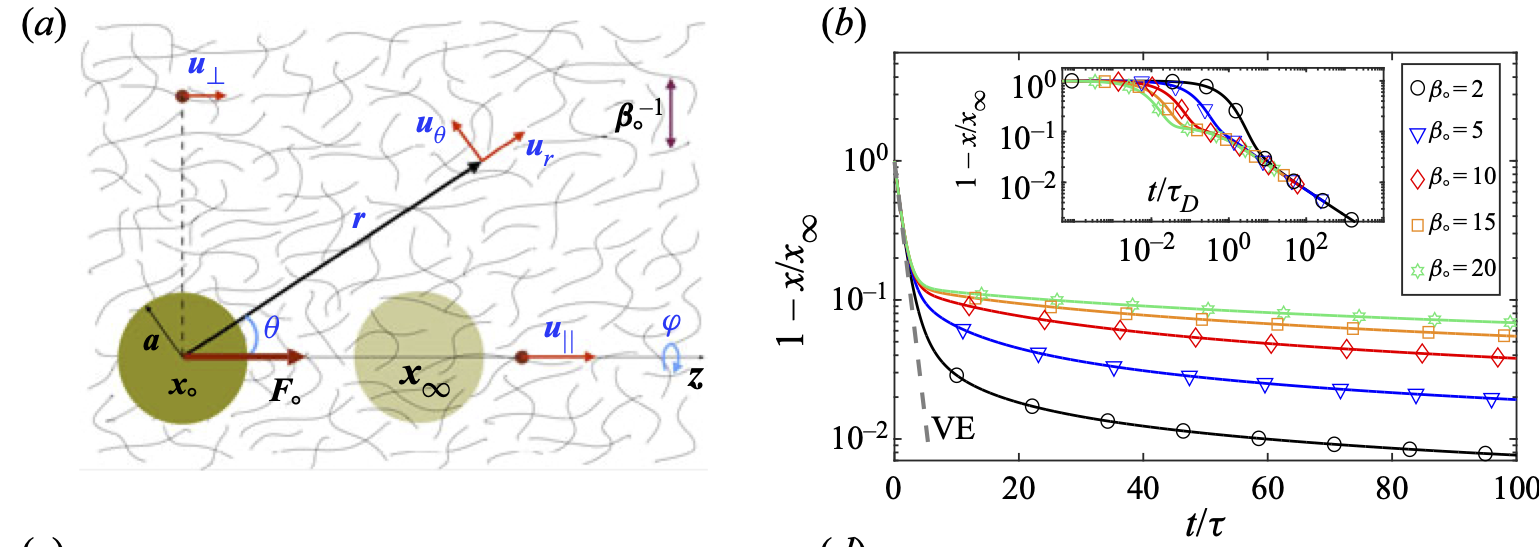
General solutions of linear poro-viscoelastic materials in spherical coordinates
by M Moradi, W Shi, E Nazockdast
In Journal of Fluid Mechanics 946, A22
The cell cytoskeleton is a dynamic assembly of semi-flexible filaments and motor proteins. The cytoskeleton mechanics is a determining factor in many cellular processes, including cell division, cell motility and migration, mechanotransduction and intracellular transport. Mechanical properties of the cell, which are determined partly by its cytoskeleton, are also used as biomarkers for disease diagnosis and cell sorting. Experimental studies suggest that in whole cell scale, the cell cytoskeleton and its permeating cytosol may be modelled as a two-phase poro-viscoelastic (PVE) material composed of a viscoelastic (VE) network permeated by a viscous cytosol. We present the first general solution to this two-phase system in spherical coordinates, where we assume that both the fluid and network phases are in their linear response regime. Specifically, we use generalized linear incompressible and compressible VE constitutive equations to describe the stress in the fluid and network phases, respectively. We assume a constant permeability that couples the fluid and network displacements. We use these general solutions to study the motion of a rigid sphere moving under a constant force inside a two-phase system, composed of a linear elastic network and a Newtonian fluid. It is shown that the network compressibility introduces a slow relaxation of the sphere and non-monotonic network displacements with time along the direction of the applied force. Our results can be applied to particle-tracking microrheology to differentiate between PVE and VE materials, and to measure the fluid permeability as well as VE properties of the fluid and the network phases.
Hydrodynamics of a single filament moving in a spherical membrane
by W Shi, M Moradi, E Nazockdast
In Physical Review Fluids, Physical Review Fluids, 7(8), 084004.
Dynamic organization of the cytoskeletal filaments and rodlike proteins in the cell membrane and other biological interfaces occurs in many cellular processes, including cell division, membrane transport, and morphogenesis. The filament dynamics are determined, in part, by their membrane-mediated hydrodynamic interactions. Previous modeling studies have considered the dynamics of a single rod on fluid planar membranes. We extend these studies to the more physiologically relevant case of a single filament moving in a spherical membrane. Specifically, we use a slender-body formulation to compute the translational and rotational resistance of a single filament of length L moving in a membrane of radius R and 2D viscosity ηm, and surrounded on its interior and exterior with Newtonian fluids of viscosities η− and η+. We first discuss the case where the filament's curvature is at its minimum κ=1/R. We show that the boundedness of spherical geometry gives rise to flow confinement effects that increase in strength with increasing the ratio of filament's length to membrane radius L/R. These confinement flows result only in a mild increase in filament's resistance along its axis, ξ∥, and its rotational resistance, ξΩ. As a result, our predictions of ξ∥ and ξΩ can be quantitatively mapped to the results on a planar membrane, when the momentum transfer length scale is modified from ℓ0=(η++η−)/ηm in planar membranes to ℓ★=(ℓ−10+R−1)−1. In contrast, we find that the drag in the perpendicular direction, ξ⊥, increases superlinearly with the filament's length when L/R>1 and ultimately ξ⊥→∞ as L/R→π. Next, we consider the effect of the filament's curvature, κ, on its parallel motion, while fixing the membrane's radius. We show that the flow around the filament becomes increasingly more asymmetric with increasing its curvature. These flow asymmetries induce a net torque on the filament, coupling its parallel and rotational dynamics. This coupling becomes stronger with increasing L/R and κ.
Cell nucleus as a microrheological probe to study the rheology of the cytoskeleton
by M. Moradi and E. Nazockdast
In Biophysical Journal, 120(9), 1542-1564.
Mechanical properties of the cell are important biomarkers for probing its architectural changes caused by cellular processes and/or pathologies. The development of microfluidic technologies has enabled measuring the cell’s mechanical properties at high throughput so that mechanical phenotyping can be applied to large samples in reasonable timescales. These studies typically measure the stiffness of the cell as the only mechanical biomarker and do not disentangle the rheological contributions of different structural components of the cell, including the cell cortex, the interior cytoplasm and its immersed cytoskeletal structures, and the nucleus. Recent advancements in high-speed fluorescent imaging have enabled probing the deformations of the cell cortex while also tracking different intracellular components in rates applicable to microfluidic platforms. We present a, to our knowledge, novel method to decouple the mechanics of the cell cortex and the cytoplasm by analyzing the correlation between the cortical deformations that are induced by external microfluidic flows and the nucleus displacements, induced by those cortical deformations, i.e., we use the nucleus as a high-throughput microrheological probe to study the rheology of the cytoplasm, independent of the cell cortex mechanics. To demonstrate the applicability of this method, we consider a proof-of-concept model consisting of a rigid spherical nucleus centered in a spherical cell. We obtain analytical expressions for the time-dependent nucleus velocity as a function of the cell deformations when the interior cytoplasm is modeled as a viscous, viscoelastic, porous, and poroelastic material and demonstrate how the nucleus velocity can be used to characterize the linear rheology of the cytoplasm over a wide range of forces and timescales/frequencies.
Mechanics of the spindle apparatus
by E. Nazockdast and S. Redemann
in Seminars in Cell & Developmental Biology (2020)
During mitosis microtubules self-organize to form a bipolar mitotic spindle structure, which positions the sister chromatids on the spindle mid-plane and separates them afterwards. Previous studies have identified many spindle associated proteins. Yet, we do not fully understand how these nanoscopic proteins lead to force generation through interactions of individual microtubules, motor proteins and chromosomes, and how a large number of these local interactions ultimately determine the structure and mechanics of the spindle in micron scale. Here we review the current understanding and open questions related to the structure and mechanics of the mitotic spindle. We then discuss how a combination of electron microscopy and computational modeling can be used to tackle some of these open questions.
Integrated 3D Tomography and Computational Modeling to Study Forces in Metaphase Spindles.
by S. Redemann and E. Nazockdast
in The FASEB Journal, 34: 1-1 (2020)
Chromosome segregation during mitosis and meiosis are fundamental processes of life. During its course a bipolar spindle assembles and initially aligns the chromosomes on a metaphase plate before they are segregated to the two arising daughter cells during anaphase. The different cellular components of mitotic and meiotic spindles: microtubules, chromosomes, motor proteins and also membranes, such as the cell cortex or nuclear envelope, must interact with each other during spindle assembly, chromosome alignment and segregation.
While we have achieved a very good understanding of signaling cascades and checkpoints that monitor and control mitosis, we are lacking an understanding on how the nano‐scale components of a spindle physically interact and generate the forces needed to faithfully align and segregate chromosomes. We have very little knowledge about the mechanics of spindles. In order to overcome the current limitations, we are generating a holistic description of mitotic and meiotic spindles in C. elegans embryos and mouse oocytes. This ambitious task will be achieved by a combination of 3D electron tomography, light microscopy and computational simulations. 3D tomography provides unprecedented detailed information about every individual microtubule within the spindle. We can measure the length, position and interactions of single microtubules with subcellular targets. In addition, we have developed tools to analyze the curvature of microtubules. Curvature originates from forces experienced by the microtubule and provides a read out of spindle intrinsic forces. The source of those forces can be determined by a combined approach of mutant analysis and computational simulations. To complement the static tomography data, we perform state‐of‐the‐art light microscopy. In conjunction with the light and electron microscopy we develop hypothesis and mechanical models of chromosome congression, alignment and segregation and test those in computational simulations and by selective depletion of proteins. We are using this approach to develop a (near) true‐to‐life model of microtubule, chromosome and membrane interactions and forces during mitosis.
An integral equation method for the simulation of doubly-periodic suspensions of rigid bodies in a shearing viscous flow
by J. Wang, E. Nazockdast, and A. Barnett
in arXiv preprint arXiv:1912.04501 (2019)
With rheology applications in mind, we present a fast solver for the time-dependent ef- fective viscosity of an infinite lattice containing one or more neutrally buoyant smooth rigid particles per unit cell, in a two-dimensional Stokes fluid with given shear rate. At each time, the mobility problem is reformulated as a 2nd-kind boundary integral equation, then discretized to spectral accuracy by the Nystr ̈om method and solved iteratively, giving typically 10 digits of accuracy. Its solution controls the evolution of particle locations and angles in a first-order system of ordinary differential equations. The formulation is placed on a rigorous footing by defining a generalized periodic Green’s function for the skew lattice. Numerically, the periodized integral operator is split into a near image sum—applied in linear time via the fast multipole method—plus a correction field solved cheaply via proxy Stokeslets. We use barycentric quadratures to evaluate particle interactions and velocity fields accurately, even at distances much closer than the node spacing. Using first-order time-stepping we simulate, eg, 25 ellipses per unit cell to 3-digit accuracy on a desktop in 1 hour per shear time. Our examples show equilibration at long times, force chains, and two types of blow-ups (jamming) whose power laws match lubrication theory asymptotics.
Hydrodynamic interactions of filaments polymerizing against obstacles
by E. Nazockdast
in Cytoskeleton, 76 (2019)
Polymerization and depolymerization of cytoskeletal filaments against cellular structures can generate forces that are key to many cellular processes, such as cell motility and chromosomes movements during cell division. Motions generated by these forces induce global cytoplasmic flows and couple the dynamics of the polymerizing filaments and other bodies immersed in the fluid through their long‐range hydrodynamic interactions (HIs). Previous theoretical and computational studies have largely ignored HIs. We use three dimensional discrete simulations to study the relationship between polymerization forces and their resulting flows and HIs. As a model system, we choose a filament that is polymerizing against an obstacle, and is embedded in a cylindrical array of parallel filaments of the same length. We consider three distinct mechanical scenarios for the filaments within the array: (a) all of the filaments are polymerizing with the same velocity; (b) they are all fixed in space, and (c) they are freely suspended. We show that each of these conditions produce their unique cytoplasmic flows and each result in differentiable polymerization forces and velocities. We also study the effect of buckling of filaments on polymerization forces and velocities and discuss the effect of HIs on the onset of buckling transition. Finally, we show that HIs result in the bundling of the buckled filaments within the array.
Dynamics of flexible fibers in viscous flows and fluids
by O. du Roure, A. Lindner, E. Nazockdast, and M. J. Shelley
in Annual Review of Fluid Mechanics, 51 (2019)
The dynamics and deformations of immersed flexible fibers are at the heart of important industrial and biological processes, induce peculiar mechanical and transport properties in the fluids that contain them, and are the basis for novel methods of flow control. Here we focus on the low–Reynolds number regime where advances in studying these fiber–fluid systems have been especially rapid. On the experimental side, this is due to new methods of fiber synthesis, microfluidic flow control, and microscope-based tracking measurement techniques. Likewise, there have been continuous improvements in the specialized mathematical modeling and numerical methods needed to capture the interactions of slender flexible fibers with flows, boundaries, and each other.
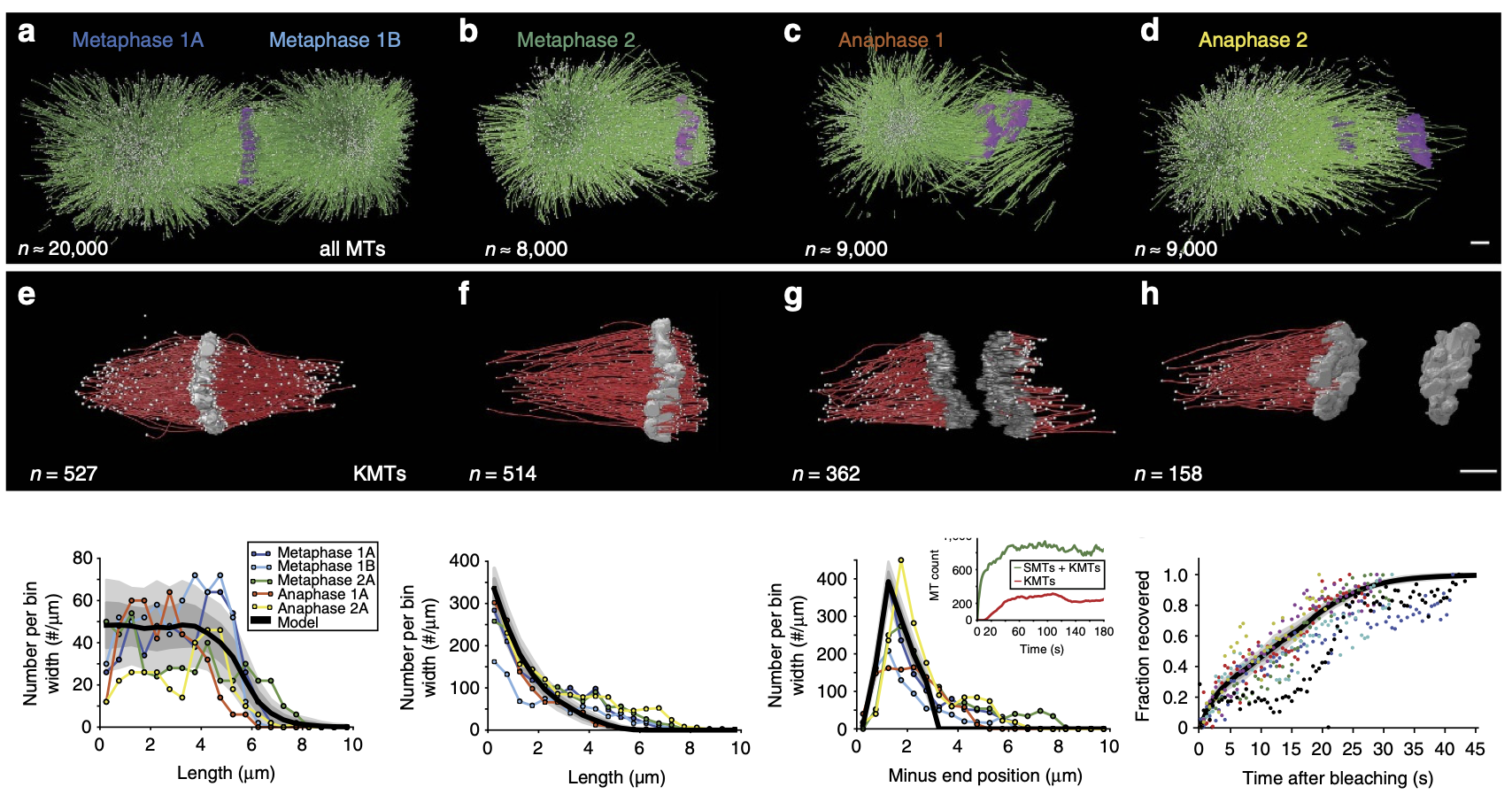
C. elegans chromosomes connect to centrosomes by anchoring into the spindle network
by S. Redemann, Johannes Baumgart, N. Lindow, M. Shelley, E. Nazockdast, A. Kratz, S. Prohaska, J. Brugués, S. Fürthauer, and Thomas Müller-Reichert
in Nature Communications, 8 (2017)
The mitotic spindle ensures the faithful segregation of chromosomes. Here we combine the first large-scale serial electron tomography of whole mitotic spindles in early C. elegansembryos with live-cell imaging to reconstruct all microtubules in 3D and identify their plus- and minus-ends. We classify them as kinetochore (KMTs), spindle (SMTs) or astral microtubules (AMTs) according to their positions, and quantify distinct properties of each class. While our light microscopy and mutant studies show that microtubules are nucleated from the centrosomes, we find only a few KMTs directly connected to the centrosomes. Indeed, by quantitatively analysing several models of microtubule growth, we conclude that minus-ends of KMTs have selectively detached and depolymerized from the centrosome. In toto, our results show that the connection between centrosomes and chromosomes is mediated by an anchoring into the entire spindle network and that any direct connections through KMTs are few and likely very transient.
Cytoplasmic flows as signatures for the mechanics of mitotic spindle positioning
by E. Nazockdast, A. Rahimian, D. Needleman, and M. Shelley
in Molecular Biology of the Cell, Vol 28 Issue 23 (2017)
The proper positioning of mitotic spindle in the single-cell Caenorhabditis elegans embryo is achieved initially by the migration and rotation of the pronuclear complex (PNC) and its two associated astral microtubules (MTs). Pronuclear migration produces global cytoplasmic flows that couple the mechanics of all MTs, the PNC, and the cell periphery with each other through their hydrodynamic interactions (HIs). We present the first computational study that explicitly accounts for detailed HIs between the cytoskeletal components and demonstrate the key consequences of HIs for the mechanics of pronuclear migration. First, we show that, because of HIs between the MTs, the cytoplasm-filled astral MTs behave like a porous medium, with its permeability decreasing with increasing the number of MTs. We then directly study the dynamics of PNC migration under various force-transduction models, including the pushing or pulling of MTs at the cortex and the pulling of MTs by cytoplasmically bound force generators. Although achieving proper position and orientation on reasonable time scales does not uniquely choose a model, we find that each model produces a different signature in its induced cytoplasmic flow. We suggest that cytoplasmic flows can be used to differentiate between mechanisms.
A fast platform for simulating semi-flexible fiber suspensions applied to cell mechanics
by E. Nazockdast, A. Rahimian, D. Zorin, and M. Shelley
in ournal of Computational Physics, 329 (2017)
We present a novel platform for the large-scale simulation of three-dimensional fibrous structures immersed in a Stokesian fluid and evolving under confinement or in free-space in three dimensions. One of the main motivations for this work is to study the dynamics of fiber assemblies within biological cells. For this, we also incorporate the key biophysical elements that determine the dynamics of these assemblies, which include the polymerization and depolymerization kinetics of fibers, their interactions with molecular motors and other objects, their flexibility, and hydrodynamic coupling. This work, to our knowledge, is the first technique to include many-body hydrodynamic interactions (HIs), and the resulting fluid flows, in cellular assemblies of flexible fibers. We use non-local slender body theory to compute the fluid–structure interactions of the fibers and a second-kind boundary integral formulation for other rigid bodies and the confining boundary. A kernel-independent implementation of the fast multipole method is utilized for efficient evaluation of HIs. The deformation of the fibers is described by nonlinear Euler–Bernoulli beam theory and their polymerization is modeled by the reparametrization of the dynamic equations in the appropriate non-Lagrangian frame. We use a pseudo-spectral representation of fiber positions and implicit time-stepping to resolve large fiber deformations, and to allow time-steps not excessively constrained by temporal stiffness or fiber–fiber interactions. The entire computational scheme is parallelized, which enables simulating assemblies of thousands of fibers. We use our method to investigate two important questions in the mechanics of cell division: (i) the effect of confinement on the hydrodynamic mobility of microtubule asters; and (ii) the dynamics of the positioning of mitotic spindle in complex cell geometries. Finally to demonstrate the general applicability of the method, we simulate the sedimentation of a cloud of semi-flexible fibers.
Forces positioning the mitotic spindle: Theories, and now experiments
by H. Wu, E. Nazockdast, M. J. Shelley, and D. J. Needleman
in Bioessays, 39 (2016)
The position of the spindle determines the position of the cleavage plane, and is thus crucial for cell division. Although spindle positioning has been extensively studied, the underlying forces ultimately responsible for moving the spindle remain poorly understood. A recent pioneering study by Garzon‐Coral et al. uses magnetic tweezers to perform the first direct measurements of the forces involved in positioning the mitotic spindle. Combining this with molecular perturbations and geometrical effects, they use their data to argue that the forces that keep the spindle in its proper position for cell division arise from astral microtubules growing and pushing against the cell's cortex. Here, we review these ground‐breaking experiments, the various biomechanical models for spindle positioning that they seek to differentiate, and discuss new questions raised by these measurements.